|
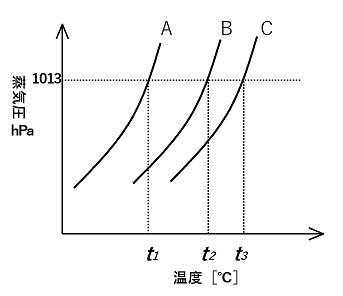
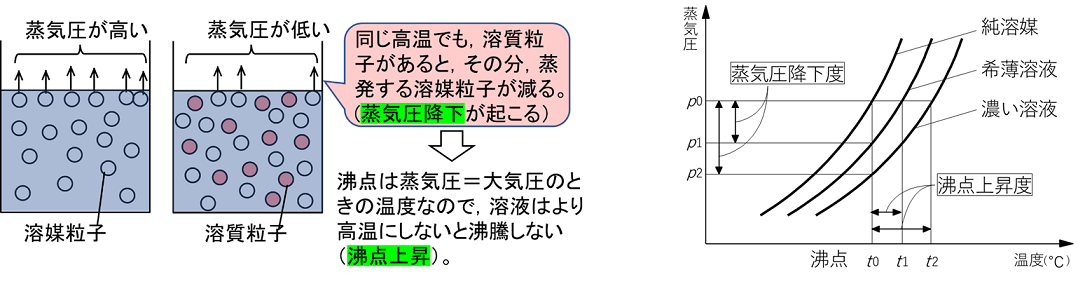
�R�@�n�t�̐����� �y���_�㏸�ƋÌœ_�~���z ���_�㏸ �t�̂ɕs�������i�������ɂ����j������n�����ƁC���̕��̗n�}���q�̊���������C�������镪�q�����邽�ߏ��C�����ቺ����B���̌��ۂ��k�@���C���~���@�l�Ƃ����B�n�t�͏��C���~���ɂ�菃�n�}�������C�����Ⴍ�Ȃ邽�߁C����������i���C������C���ɂ���j�̂ɏ��n�}�����M�������Ȃ���Ȃ炸�C������k�@���_�㏸�@�l�Ƃ����B���_�㏸�x�͗n�����q�̎�ނɊW�Ȃ��C�Z�x�i���ʃ����Z�x�j�ɔ�Ⴗ���B |
|||
 |
|||
|
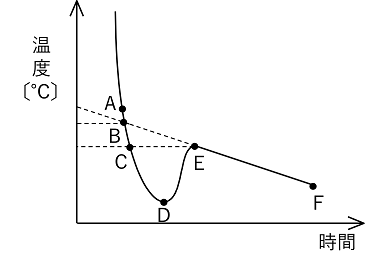
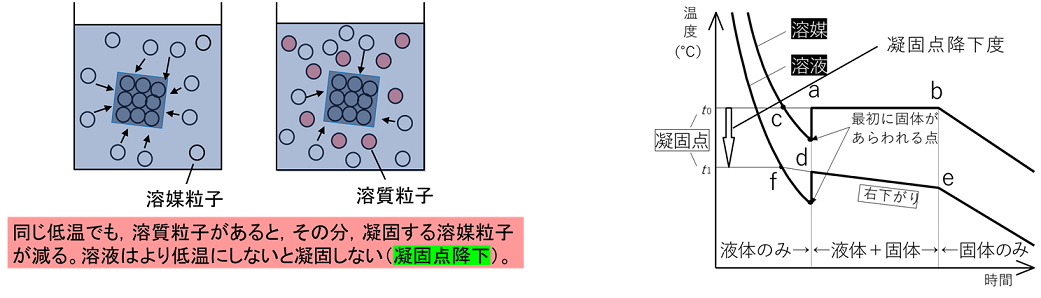
�Ìœ_�~�� �n�}�ɕs�������̗n����n������ƁC�n�t�̋Ìœ_�͗n�}�����Ⴍ�Ȃ�B������k�@�Ìœ_�~���@�l�Ƃ����C�Ìœ_�~���x�͗n�����q�̎�ނɊW�Ȃ��C�Z�x�i���ʃ����Z�x�j�ɔ�Ⴗ���B�܂��C�n�t�̏ꍇ�C�n�}����ɋÌł���̂ŁC�n�t�̔Z�x�͂������ɔZ���Ȃ��Ă����B���̂��߁C����ɋÌœ_�~�����N����C�E���̃O���t��d�`e�͉E������ɂȂ�B�܂��C�t�̂��p���Ă����ƁC�E���̃O���t�̂悤�ɋÌœ_�ȉ��ɂȂ��Ă������ɂ͋Ìł��Ȃ��B���̌��ۂ��k�@�ߗ�p�@�l�Ƃ����C�Ìł���ƃG�l���M�[�̍������(�t��)����Ⴂ���(�ő�)�֕ω�����̂ŔM(�ÌŔM)���������ĉ��x���㏸����B |
|||
 |
|||
|
���ʃ����Z�x�kmol/kg�l �n�}1kg������ɗn���Ă���n���̕����ʂ����ʃ����Z�x�Ƃ����B�n�t�̑̐ρi���x�ɂ���ĕω�����j��p���Ă��Ȃ��̂ŁC���x�ω����Ƃ��Ȃ����ۂŗp������B �i��j�@�A�fCO(NH2)2�i���q��60.0�j6.0g��200g�ɗn�������n�t�̎��ʃ����Z�x�kmol/kg�l �A�f��mol�^����kg�@���@6.0�^60.0�@�~�@1�^0.200�@���@0.50�kmol/kg�l �n�t�̔Z�x�ƕ��_�㏸�C�Ìœ_�~���̑傫��(���_�㏸�x�C�Ìœ_�~���x) �s�������̔�d������1mol/kg�̗n�t�̕��_���C���n�}�̕��_�����ǂꂾ���������������l���������_�㏸Kb�Ƃ����B���l�ɁC�s�������̔�d������1mol/kg�̗n�t�̋Ìœ_�~���̑傫���������Ìœ_�~��Kf�Ƃ����B�����̒l�͗n�}�̎�ނɌŗL�̒l�ƂȂ�i���_�㏸�C�Ìœ_�~���͗n�����q�̎�ނɊW�Ȃ��C�n���̎��ʃ����Z�xm�ɔ�Ⴗ��̂Łj�B���ʃ����Z�xm mol/kg�n�t�̕��_�㏸�̑傫��(���_�㏸�x)��T��Ìœ_�~���̑傫��(�Ìœ_�~���x)��T�f �͎��̂悤�ɕ\�����B�k�@��T�@���@Kb �~ m�@�l�C�k�@��T�f�@���@Kf �~ m�@�l ��� �@���̖₢�ɓ�����B�������C���̃����Ìœ_�~��Kf��1.85K�kg/mol�C���Y�f�̃������_�㏸Kb��2.3K�kg/mol�Ƃ���B (1)�@�G�`�����O���R�[��C2H6O2�i���q��62�j�̐��n�t�́C�s���t�̖��O�ŗp�����Ă���B���܁C��100g�ɃG�`�����O���R�[����40g�n�������s���t�͉����ŋÌł��邩�B (2)�@�����̌���0.32g����Y�f��24.32g�ɗn�������n�t�̕��_�́C�����ȓ��Y�f����0.118�����������B�����̕��q�ʂ͂����炩�B (1)�@��T�f��Kf�~m�C��T�f��1.85�~(40/62)�~�i1/0.100�j��11.9��12�k���l�C���̋Ìœ_��0���Ȃ̂ŁC�Ìœ_�~���ǂ́C�| (2)�@�����̕��q�ʂ�x�Ƃ��C��T��Kb�~m ���C0.118��2.3�~(0.32/x)�~(1/0.02432)�Cx��2.56�~102��2.6�~102 |
|||
|
��� �@�E�̐}�̓X�N���[�XC12H22O11�̊n�t���p���Ă����ꍇ�́C��p���ԂƉ��x�̊W����������p�Ȑ��ł���B���̊e�₢�ɓ�����B |
|||
|
|||
|
(1)�@B�@�@(2)�@�ÌŔM�����o����邩��@�@ (3)�@�n�}���Ìł���ƁC�c�����n�t�̔Z�x���Z���Ȃ�C����ɋÌœ_�~�����N���邩��B�@�@(4)�@�|0.11�� |
|||
|
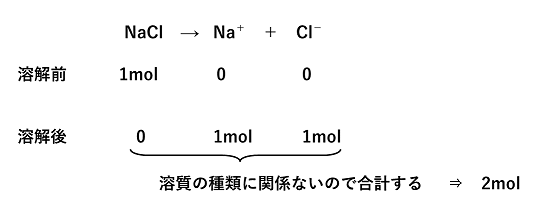
�n�����d�����i�n�t���œd�����镨���j�̏ꍇ |
 |
||
|
|||
|
|||
|
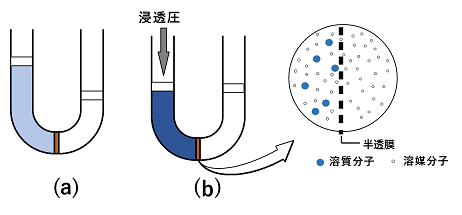
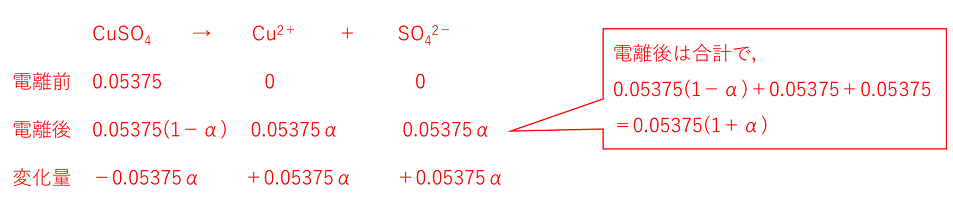
�E�̐}�̂悤�ɁC���n�}�Ɨn�t��ڐG������ƁC�n�}���n�t�̕��Z�����C�n�t���̉t�ʂ��オ��ia�j�B���E�̉t�ʂ̍�������������ɂ́C�n�t���Ɉ��̈��͂�������K�v������ib�j�B���̈��͂�n�t�̐Z�����Ƃ����B �n�t�̐Z�����͗n���̎�ނɊW�Ȃ��C�n���Ă���n�����q�i���q,�C�I���Ȃǁj�̃����Z�x�i���ʃ����Z�x�ł͂Ȃ��j�ɔ�Ⴕ�C��Ή��x�ɔ�Ⴗ���B���̊W�́C�C�̂̏�ԕ������ipV=nRT�j�Ɠ������ŕ\�����Ƃ��ł��C�Z���������Ƃ��āC��V=nRT�ƕ\���B ����@0.10mol/L�̃u�h�E��C6H12O6�i���q��180�j���n�t�Ɠ����Z�������������J���V�E��CaCl2�i����111�j���n�t��100mL����ɂ͉����J���V�E������g���ɗn�����悢���B�����J���V�E���͊��S�ɓd��������̂Ƃ���B �����J���V�E�����n�t�́C�d��������̃����Z�x���l����B�K�v��CaCl2��xg�Ƃ���ƁC�����Z�x��x/111�~(1/0.100)�kmol/L�l�B���̒l�͓d������O�̃����Z�x�Ȃ̂ŁC�d����̃����Z�x���l����BCaCl2�̓d���́CCaCl2��Ca2�{�{2Cl�|�Ȃ̂ŁCCa2�{��Cl�|�̍��v��CaCl2��3�{mol�ɂȂ�BCaCl2 xg�ł́C�����Z�x��x/111�~(1/0.100)�~3�kmol/L�l�ƂȂ�B�܂��C�n���̎�ނɊW�Ȃ��Z�����͗n���̃����Z�x�ɔ�Ⴗ��̂ŁC���̗n�t�̃����Z�x�́C0.10mol/L�ƂȂ�̂ŁC0.10��x/111�~(1/0.100)�~3�����藧�Bx��0.37�kg�l ����@���_��(�U)������CuSO4�i����160�j��8.6g��n������500mL�Ƃ������n�t��20���ɂ�����Z�����𑪒肵���Ƃ���C3.37�~105Pa�ł������B���_��(�U)�̓d���x�����߂�B�C�̒萔R=8.3�~103Pa�L/(K�mol) CuSO4 8.6g�̓d���O�̕����ʂ́C8.6/160��0.05375�kmol/L�l�BCuSO4�̓d���x�����Ƃ���ƁC0.05375���������d������̂œd������l����Ǝ��̂悤�ɂȂ�C�d�����0.05375(1�{��)mol/L�ƂȂ�B |
|||
 |
|||
|
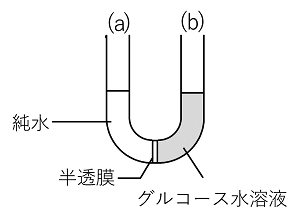
������C��V=nRT�ɑ�����ă������߂�ƁC3.37�~105�~0.500��0.05375(1�{��)�~8.3�~103�~293�C����0.289��0.29 ����@�}�̂悤�ɁCU���ǂ̒��������Ŏd��C(a)�ɂ͏����Ȑ����C(b)�ɂ̓O���R�[�X�n�t���C�����ɗ����̉t�ʂ����������ɂȂ�悤�ɓ���C27���ɂȂ�悤�ɕۂ��ĕ��u�����B |
|||
|
|||
|
(1)�@(b)�@�@(2)�@ ��V=nRT���C���~0.200��(1.2/180)�~8.3�~103�~300��8.3�~104�kPa�l ����@����^���p�N��0.059g��n���������n�t10mL������B���̐��n�t�̐Z������27����2.1�~102Pa�ł������B���̃^���p�N���̕��q�ʂ͂����炩�B�C�̒萔R=8.3�~103Pa�L/(K�mol) ���q�ʂ�M�Ƃ���ƁC��V=nRT���C2.1�~102�~0.010��(0.059/M)�~8.3�~103�~300��6.99�~104��7.0�~104 |
|||
 |
|||